
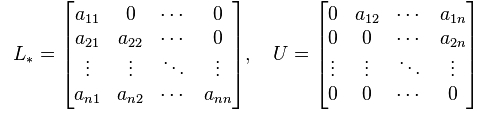
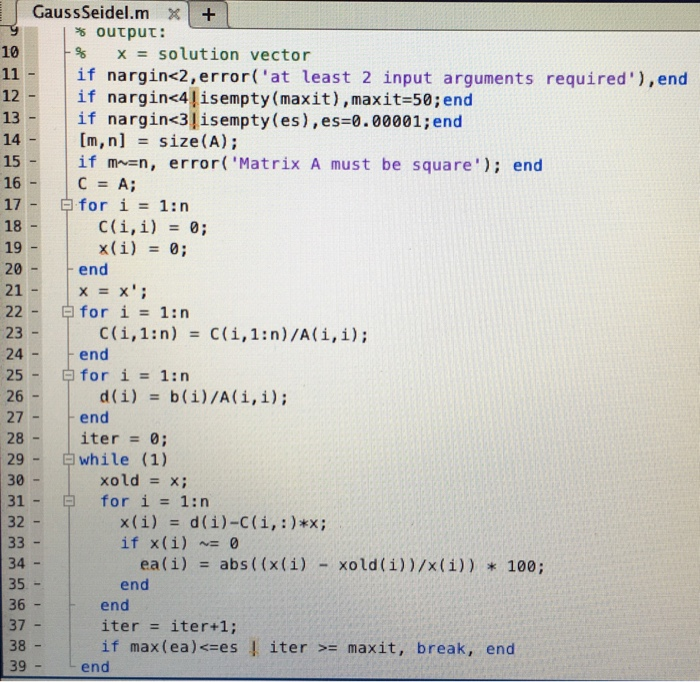
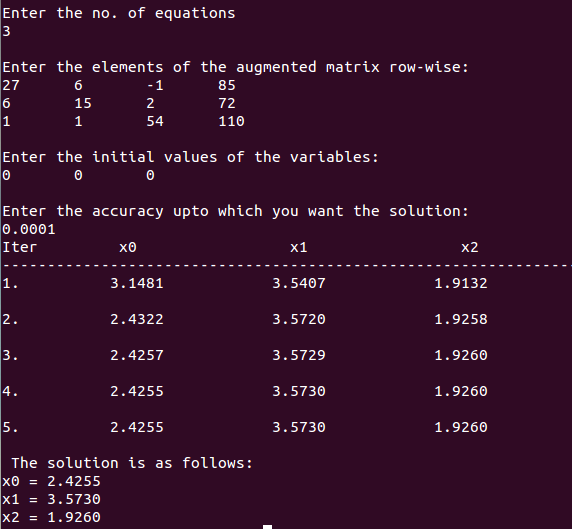
So, to understand the complete physical phenomena, the mathematical modeling comes into account by means of partial differential equations (PDEs), that shows an exceptional performance in science and engineering. In any branch of natural sciences, there exists a small number of problems, that can be solved in a direct way. The importance of the nonlinear phenomena of differential equations (DEs) in sciences (biology, physics and chemistry) is significant. įunding: There is no source of funding (financial or material support) for my study.Ĭompeting interests: The authors have declared that no competing interests exist. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.ĭata Availability: All relevant data underlying this study can be found, in the form of exact solutions of seventh order KdV-type, differential equations, theorems and definitions, at the following locations. Received: AugAccepted: DecemPublished: January 22, 2021Ĭopyright: © 2021 Saleem et al. PLoS ONE 16(1):Ĭhina University of Mining and Technology, CHINA From the above, we know that we get an upper triangular matrix after we conduct the Gauss Elimination.Citation: Saleem S, Hussain MZ, Aziz I (2021) A reliable algorithm to compute the approximate solution of KdV-type partial differential equations of order seven. A solution to a system of linear equations is an \(x\) in \(\]īut how can we calculate and get the \(L\) and \(U\) matrices? There are different ways to get the LU decomposition, let’s just look one way using the Gauss Elimination method. Recall that this means there are \(m\) equations and \(n\) unknowns in our system. Solutions to Systems of Linear Equations ¶Ĭonsider a system of linear equations in matrix form, \(Ax=y\), where \(A\) is an \(m \times n\) matrix. Introduction to Machine LearningĪppendix A. Ordinary Differential Equation - Boundary Value ProblemsĬhapter 25. Predictor-Corrector and Runge Kutta MethodsĬhapter 23. Ordinary Differential Equation - Initial Value Problems Numerical Differentiation Problem Statementįinite Difference Approximating DerivativesĪpproximating of Higher Order DerivativesĬhapter 22. Least Square Regression for Nonlinear Functions Least Squares Regression Derivation (Multivariable Calculus) Least Squares Regression Derivation (Linear Algebra) Least Squares Regression Problem Statement Solve Systems of Linear Equations in PythonĮigenvalues and Eigenvectors Problem Statement Linear Algebra and Systems of Linear Equations Errors, Good Programming Practices, and DebuggingĬhapter 14. Inheritance, Encapsulation and PolymorphismĬhapter 10. Variables and Basic Data StructuresĬhapter 7.
Python Programming And Numerical Methods: A Guide For Engineers And ScientistsĬhapter 2.


 0 kommentar(er)
0 kommentar(er)
